Дробь - это что такое? Виды дробей. Новые понятия и связи между ними. Свойства абсолютной величины
Пусть требуется измерить длину отрезка x с помощью единичного отрезка e (рис.27). При измерении оказалось, что отрезок x состоит из трех отрезков, равных e, и отрезка, который короче отрезка e. В этом случае длина отрезка x не может быть выражена натуральным числом.
Однако если отрезок e разбить на 4 равные части, то отрезок x окажется состоящим из 14 отрезков, равных четвертой части отрезка e. И тогда, говоря о длине отрезка x, мы должны указать два числа 4 и 14: четвертая часть отрезка e укладывается в отрезке точно 14 раз. Поэтому условились длину отрезка x записывать в виде , где E – длина единичного отрезка e, а символ называть дробью.
В общем виде понятие дроби определяют так.
Пусть даны отрезок
x
и единичный отрезок
e
, длина которого
E
. Если отрезок
x
состоит из
m
отрезков, равных
n
-ой части отрезка
e
, то длина отрезка
x
может быть представлена в виде , где символ называют дробью (и читают “эм энных”).
В записи дроби числа m и n – натуральные, m называется числителем , n – знаменателем дроби.
Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.
Ранее показано, что четвертая часть отрезка e уложилась в отрезке x
точно 14 раз. Очевидно, это не единственный вариант выбора такой части отрезка e
, которая укладывается в отрезок x
целое число раз. Можно взять восьмую часть отрезка e
, тогда отрезок x
будет состоять из 28 таких частей и его длина будет выражаться дробью . Можно взять шестнадцатую часть отрезка
e
, тогда отрезок x
будет состоять из 56 таких частей и его длина будет выражаться дробью .
Вообще длина одного и того же отрезка x при заданном единичном отрезке e может выражаться различными дробями, причем, если длина выражена дробью , то она может быть выражена и любой дробью вида , где
k
– натуральное число.
Теорема. Для того чтобы дроби и выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство .
Доказательство этой теоремы мы опускаем.
Две дроби и называются равными, если .
Если дроби равны, то пишут .
Например, , так как , а , потому что , а и .
Из сформулированных выше теоремы и определения следует, что две дроби равны тогда и только тогда, когда они выражают длину одного и того же отрезка.
Нам известно, что отношение равенства дробей рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности.
Из определения равных дробей вытекает основное свойство дроби. Напомним его.
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится дробь, равная данной.
На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю.
Сокращение дробей – это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем.
Если числитель и знаменатель дроби одновременно делятся только на единицу, то дробь называют несократимой . Например, – несократимая дробь, так как её числитель и знаменатель делятся одновременно только на единицу, т.е D(5, 17) = 1.
Подробно разобрано основное свойство дроби , дана его формулировка, приведено доказательство и поясняющий пример. Также рассмотрено применение основного свойства дроби при сокращении дробей и приведении дробей к новому знаменателю.
Навигация по странице.
Основное свойство дроби – формулировка, доказательство и поясняющие примеры
Все обыкновенные дроби обладают одним очень важным свойством, которое называют основным свойством дроби. Сформулируем основное свойство дроби : если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
Запишем основное свойство дроби в буквенном виде: для натуральных чисел a , b и m справедливы равенства и .
Приведем доказательство основного свойства дроби . Равенства (a·m)·b=(b·m)·a и (a:m)·b=(b:m)·a справедливы в силу свойств умножения натуральных чисел и свойств деления натуральных чисел, тогда дроби и , а также и равны по определению (смотрите равные и неравные дроби).
Давайте рассмотрим пример, иллюстрирующий основное свойство дроби. Пусть у нас есть квадрат, разделенный на 9 «больших» квадратов, а каждый из этих «больших» квадратов разделен на 4 «маленьких» квадрата. Таким образом, можно также говорить, что исходный квадрат разделен на 4·9=36 «маленьких» квадратов. Закрасим 5 «больших» квадратов. При этом закрашенными окажутся 4·5=20 «маленьких» квадратов. Приведем рисунок, отвечающий нашему примеру.

Закрашенная часть составляет 5/9 исходного квадрата, или, что то же самое, 20/36 исходного квадрата, то есть, дроби 5/9 и 20/36 равны: или . Из этих равенств, а также из равенств 20=5·4 , 36=9·4 , 20:4=5 и 36:4=9 следует, что и .
Для закрепления разобранного материала рассмотрим решение примера.
Числитель и знаменатель некоторой обыкновенной дроби умножили на 62 , после чего числитель и знаменатель полученной дроби разделили на 2 . Равна ли полученная дробь исходной?
Умножение числителя и знаменателя дроби на любое натуральное число, в частности на 62 , дает дробь, которая в силу основного свойства дроби, равна исходной. Основное свойство дроби позволяет утверждать и то, что после деления числителя и знаменателя полученной дроби на 2 получится дробь, которая будет равна исходной дроби.
да, полученная дробь равна исходной.
Применение основного свойства дроби
Основное свойство дроби в основном применяется в двух случаях: во-первых, при приведении дробей к новому знаменателю, и, во-вторых, при сокращении дробей.
Приведение дроби к новому знаменателю – это замена исходной дроби равной ей дробью, но с большим числителем и знаменателем. Для приведения дроби к новому знаменателю и числитель, и знаменатель дроби умножается на некоторое натуральное число, при этом, согласно основному свойству дроби, получается дробь, равная исходной, но с другим числителем и знаменателем. Без приведения дробей к новому знаменателю не обойтись при выполнении действий с обыкновенными дробями.
Основное свойство дроби позволяет проводить сокращение дробей, и в результате переходить от исходной дроби к равной ей дроби, но с меньшим числителем и знаменателем. Сокращение дроби заключается в делении числителя и знаменателя исходной дроби на любой отличный от единицы положительный общий делитель числителя и знаменателя (если таких общих делителей нет, то исходная дробь несократима, то есть, не подлежит сокращению). В частности, деление на наибольший общий делитель приведет исходную дробь к несократимому виду.
www.cleverstudents.ru
Основное свойство дроби
Чтобы сравнить, сложить или вычесть обыкновенные дроби с разными знаменателями, их нужно вначале привести к одинаковому (одному) знаменателю.
Для этого число, от которого взята часть долями (количество долей числа определяет знаменатель), разбивается на большее число долей так, чтобы все знаменатели дробей были кратны между собой.
Например, нужно сравнить, сложить или вычесть дроби и. Рассмотрим на рисунке дробление на доли (1 разделили на 4 части и 1 разделили на 2 части), за целое принимается 1.
Разделив на 2 доли, получаем наглядное сравнение.
Значит, , так как в доли содержится 2 доли по Запишем: . По правилам арифметики: Выделим простые множители в числителе и знаменателе:
Приведенные рисунки позволяют вывести правило, называемое основным свойством дроби .
Правило. Числитель и знаменатель дроби можно умножать или делить на одно и то же натуральное число, от чего величина дроби не изменяется.
Если числитель новой дроби представить произведением (или частным) первой дроби и любого натурального числа, а знаменатель новой дроби - произведением (или частным) знаменателя первой дроби и того же числа, то новая дробь сохраняет при вычислении произведений (или частных) значение (величину) исходной дроби, поэтому между заданной и полученной дробью можно ставить знак равенства.

Можно записать основное свойство дроби при умножении числителя и знаменателя дроби на число:
![]()
Можно записать основное свойство дроби при делении числителя и знаменателя дроби на число:
Сокращение дробей
С помощью дробей одну и ту же часть целого предмета можно записать разными способами.
На рисунке закрашена половина круга
Таким образом, все эти дроби равны.
 Дробь
Дробь
Для удобства дополнительный множитель записывают на наклонной черте справа над дробью.

Вернёмся ещё раз к нашим дробям и запишем их в другом порядке.

Дробь, равную данной, можно получить, если числитель и знаменатель дроби одновременно разделить на одно и то же число, не равное нулю.
Такое преобразование дроби называют сокращением дроби .
Сокращение дроби обычно записывают следующим образом.
Числитель и знаменатель зачёркиваются чёрточками, и рядом с ними записываются результаты деления (частные) числителя и знаменателя на одно и то же число.
Число, на которое делили числитель и знаменатель, держим в уме.
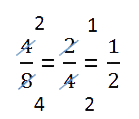
В нашем примере мы сокращали (то есть делили и числитель, и знаменатель) дробь на двойку, которую держали в уме.
Сокращение дроби можно проводить последовательно.

Сформулируем основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
Запишем это свойство в виде буквенных выражений.
 , где « a », « b » и « k » - натуральные числа.
, где « a », « b » и « k » - натуральные числа.
Основное свойство дроби. Сокращение дробей. Равенство дробей.
Равенство дробей.
Данная тема достаточно важна на основных свойствах дробей основана вся дальнейшая математика и алгебра. Рассмотренные свойства дробей, не смотря на свою важность очень просты.
Чтобы понять основные свойства дробей рассмотрим окружность.
 На окружности видно, что 4 части или доли закрашены из восьми возможных. Запишем полученную дробь \(\frac \)
На окружности видно, что 4 части или доли закрашены из восьми возможных. Запишем полученную дробь \(\frac \)

На следующей окружности видно, что закрашена одна часть из двух возможных. Запишем получившеюся дробь \(\frac \)
Если внимательно приглядимся, то увидим, что в первом случае, что во втором случае у нас закрашено половина круга, поэтому полученные дроби равны \(\frac = \frac \), то есть это одно и тоже число.
Как же это доказать математически? Очень просто, вспомним таблицу умножения и распишем первую дробь на множители.
Что мы сделали? Расписали числитель и знаменатель на множители \(\frac > >\), а потом разделили дроби \(\frac \cdot \color \). Четыре поделить на четыре это 1, а единица умноженное на любое число это и есть само число. То что мы проделали в приведенном примере называется сокращением дробей .
Посмотрим еще один пример и сократим дробь.
Мы опять расписали числитель и знаменатель на множители и одинаковый числа в числители и знаменатели сократили. То есть два деленное на два дало единицу, а единица умноженная на любое число дает тоже самое число.
Основное свойство дроби.
Отсюда следует основное свойство дроби:
Если и числитель, и знаменатель дроби умножить на одно и тоже число (кроме нуля), то величина дроби не изменится.
Также можно дроби числитель и знаменатель делить на одно и тоже число одновременно.
Рассмотрим пример:
Если и числитель, и знаменатель дроби делить на одно и тоже число (кроме нуля), то величина дроби не изменится.
Дроби у которых есть и в числители, и в знаменатели общие простые делители называются сократимыми дробями .
Пример сократимой дроби: \(\frac , \frac , \frac , \frac , …\)
Так же есть и несократимые дроби .
Несократимая дробь – это дробь у которые нет в числители и знаменатели общих простых делителей.
Пример несократимой дроби: \(\frac , \frac , \frac , \frac , …\)
Любое число можно представить в виде дроби, потому что любое число делиться на единицу, например:
Вопросы к теме:
Как вы думаете любую можно дробь сократить или нет?
Ответ: нет, бывают сократимые дроби и несократимые дроби.
Проверьте справедливо ли равенство: \(\frac = \frac \)?
Ответ: распишем дробь \(\frac = \frac = \frac \)
, да справедливо.
Пример №1:
а) Найдите дробь со знаменателем 15, равную дроби \(\frac \)
.
б) Найдите дробь с числителем 8, равную дроби \(\frac \)
.
Решение:
а) Нам нужно чтобы в знаменателе стояло число 15. Сейчас в знаменателе число 3. На какое число нужно умножить цифру 3, чтобы получить 15? Вспомним таблицу умножения 3⋅5. Нам надо воспользоваться основным свойством дробей и умножить и числитель, и знаменатель дроби \(\frac \)
на 5.
б) Нам нужно чтобы в числителе стояло число 8. Сейчас в числители стоит число 1. На какое число нужно умножить цифру 1, чтобы получить 8? Конечно, 1⋅8. Нам надо воспользоваться основным свойством дробей и умножить и числитель, и знаменатель дроби \(\frac \) на 8. Получим:
Пример №2:
Найдите несократимую дробь, равную дроби: а)\(\frac \),
б) \(\frac \)
.
Пример №3:
Запишите число в виде дроби: а) 13 б)123
Урок по теме равенство дробей, 5 класс, учебник Никольский С. М. и др.
Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Напоминаем, что в соответствии с профстандартом педагога (утверждён Приказом Минтруда России), если у Вас нет соответствующего преподаваемому предмету образования, то Вам необходимо пройти профессиональную переподготовку по профилю педагогической деятельности . Сделать это Вы можете дистанционно на сайте проекта «Инфоурок» и получить диплом с присвоением квалификации уже через 2 месяца!
Только сейчас действует СКИДКА 50% для всех педагогов на все 111 курсов профессиональной переподготовки! Доступна рассрочка с первым взносом всего 10%, при этом цена курса не увеличивается из-за использования рассрочки!
Карточка для практической работы.docx
Карточка 1
Карточка 2



Задание. Посмотрите на рисунки и сделайте вывод о равенстве дробей.
Подсказка 1. Какая часть кругов и квадратов закрашена?
Подсказка 1. Запишите дроби, обозначающие закрашенную часть каждой фигуры.
Подсказка 2. Сделайте вывод о равенстве полученных дробей.
Выбранный для просмотра документ Технологическая карта урока математики в 5 классе.docx
Технологическая карта урока математики в 5 классе
Тема урока: «Равенство дробей» (учебник «Математика 5», Никольский С. М., Потапов М. К. и др.)
Цели (задачи) урока:
— познакомить учащихся с основным свойством дроби, показать его применение для сокращения дробей;
— учить сокращать дроби и определять несократимые;
— развивать умение применять математические знания для решения практических задач;
— воспитывать культуру поведения при групповой работе;
— воспитывать интерес к предмету.
— знать основное свойство дроби, определение сокращения дробей и несократимой дроби;
— уметь приводить дроби к новому знаменателю, сокращать дроби;
понимать смысл поставленной задачи; инициатива, находчивость, активность при решении математических задач;
— умение видеть математическую задачу в контексте проблемной ситуации;
— понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Тип урока, педагогическая технология
Изучение нового, технология проблемного диалога.
Доска, мел, компьютер с мультимедийным проектором, интерактивная доска, раздаточные материалы, ролик с физкультминуткой, листы самооценки
Опорные понятия, термины
Новые понятия и связи между ними
Сократимая дробь, несократимая дробь
Контроль, самоконтроль на уроке
Используемые методы, приёмы, формы
Универсальные учебные действия
I . Организационный момент.
Тетради вы получили на перемене, так как домашнее задание все выполнили и вопросов по нему не возникло.
Проявление доброжелательного внимания.
Проверка наличия учебных средств, рациональное размещение на парте
Взаимное приветствие, контроль присутствующих, проверка готовности кабинета к уроку.
Готовность учащихся к обучению, деятельности
II . Актуализация знаний
Давайте вспомним то, что мы изучали на прошлых уроках. Что мы изучали? (дроби)
1. Что записывается под чертой дроби?
2.Что он показывает?
3.Что записывается над чертой дроби?
4.Что он показывает?
5.Какое действие заменяет черта дроби?
6. Найти ¼ от 120.
(на сколько частей разделили целое)
(сколько таких частей взяли)
Тестовые задания, ответы даются с помощью сигналов разного цвета
Регулятивные: волевая саморегуляция.
Личностные : действие смыслообразования, мотивация учения
планирование учебного сотрудничества с учителем и со сверстниками.
Готовность к открытию нового
III . Постановка проблемы
Сейчас я предлагаю вам решить такую задачу-сказку. Проблемная задача
В некотором царстве, в некотором государстве жил – был царь, и было у него три сына. Вот как–то созвал он своих сыновей и говорит: “Сыночки вы мои милые, видно, пришло мне время уходить на покой. Собрал я вас, чтобы разделить между вами наследство, наше царство – государство. Да вот беда – учёные–то наши видно что–то напутали. Тебе, старший мой сын, отписано нашего государства, тебе, средний мой сын, — , а тебе, младшенький мой — ”. Возмутился младший сын: “За что меня–то обделили?” И рассорились братья меж собой. А царь издал указ “Кто сумеет ошибку найти и сынов моих помирить, того ждёт царская награда. ”
Ребята, а мы с вами можем помирить царя и его сыновей? Что для этого нам нужно выяснить?
Значит, чему, вероятно, мы будем учиться на сегодняшнем уроке?
И давайте попробуем сформулировать тему нашего урока.
Откройте свои тетради, подпишите в них число, классная работа и тему урока «Равенство дробей».
(Равны дроби или нет)
(Узнавать, равны дроби или нет)
формулирование цели урока
Постановка проблемы, формулировка цели, темы урока
IV . Планирование решения учебной задачи
А сейчас помогите мне составить план урока, то есть определить то, чем мы будем заниматься.
(1. Научиться определять, равны дроби или нет.
Регулятивные: планирование познавательной деятельности
Составление плана урока
Древняя китайская поговорка гласит: «Я слышу и забываю, я вижу и запоминаю, я делаю и понимаю». И для того чтобы понять тему сегодняшнего урока, проведем практическую работу.
У каждого из вас на столе лежат карточки.
Возьмите карточку 1.
Поработаем с квадратом. Разделите квадрат на четыре равные части и закрасьте три из них. Какая часть
квадрата оказалась закрашенной?
Каждую четверть квадрата разделите на 4 части. На сколько частей теперь
А сколько таких частей в трех закрашенных четвертях квадрата?
Какая часть квадрата закрашена?
Что же вы можете сказать о дробях ¾ и 12/16?
Возьмите карточку 2 и ответьте на вопросы:
1. Какая часть от целого изображена и закрашена на рисунках? Подпишите под каждым кругом, какая его часть закрашена.
Что вы можете сказать об этих дробях?
Значит, одну и ту же часть можно записать по–разному.
Давайте внимательно посмотрим на эти дроби. Как можно из одной дроби получить другую, например, как из ¾ получить 12/16?
А как из 4/8 получить 2/4, ½?
Делаем вывод, формулируем правило:
Ребята, свойство, которое мы с вами сейчас сформулировали, очень важное и называется оно основным свойством дроби.
Запишите, пожалуйста, с доски правило и формулы.
![]()
a, b, c – натуральные. Обратите на это внимание, это очень важно, т. к. на 0 делить нельзя.
(умножить числитель и знаменатель на 4)
(поделить числитель и знаменатель на 2, на 4)
(При умножении и делении числителя и знаменателя дроби на одно и то же число (кроме 0) её величина не изменится .)
Познавательные: сравнение, обобщение, формулирование вывода
Выполнение практической работы. Формулировка основного свойства дроби
VI . Формирование способа действия
Представьте следующие дроби: в виде дроби со знаменателем 12.
Представьте следующие дроби: ![]() в виде дроби со знаменателем 3.
в виде дроби со знаменателем 3.
Письменно: замените дроби ![]() равными им дробями с меньшими знаменателями. Ребята, преобразование, которое мы с вами только что выполняли, называется сокращением дробей
.
равными им дробями с меньшими знаменателями. Ребята, преобразование, которое мы с вами только что выполняли, называется сокращением дробей
.
Запишите с экрана, что такое сокращение дроби.
Разделить числитель и знаменатель одной дроби на одно и то же число, значит сократить её.
Если числитель и знаменатель дроби не имеют общих простых делителей, то эта дробь называется несократимой.
Выполняют задания. Записывают в тетради, что такое сокращение дробей и что такое несократимая дробь
Регулятивные: коррекция действий и результатов
Первичное усвоение и применение основного свойства дроби, определения сокращения дробей, несократимой дроби
VII . Формирование новых знаний и способов действия
Давайте теперь вернёмся к плану нашего урока. Что мы уже сделали? Что ещё нужно сделать?
Отлично. Сейчас я предлагаю вам немножко поиграть.
Объединимся в две группы. Первая группа (I ряд) из всех предложенных дробей
выберет дроби, равные 1/2, а вторая группа (II ряд) — дроби, равные 1/3.
А теперь проверим, как вы справились с заданием.
Теперь вернёмся к сказочной задаче, которая вызвала у нас затруднения в начале урока. Скажите, теперь вы можете ответить на вопрос задачи: напутали ли что-то советники царя?
А сейчас ещё немного потренируемся. Возьмите в руки листочки с тренировочными упражнениями, внимательно прочтите задания и выполняйте их.
(Научились определять, равны ли дроби. Нужно потренироваться)
(Теперь можем. Наследство поделили поровну, т. к. представленные дроби равны)
Тренировочные упражнения на карточках
Работа с интерактивной доской. Работа в группах
Коммуникативные: определение целей и функций участников в группе; инициативное сотрудничество; контроль, коррекция, оценка действий партнера.
Применение и отработка новых знаний и способов действия
VIII . Подведение итогов урока, рефлексия, домашнее задание
Изучая царицу всех наук - математику, в определенный момент все сталкиваются с дробями. Хотя это понятие (как и сами виды дробей или математические действия с ними) совсем несложное, к нему нужно относиться внимательно, ведь в реальной жизни за пределами школы оно очень пригодится. Итак, давайте освежим свои знания о дробях: что это, для чего нужно, какие виды их бывают и как совершать с ними различные арифметические действия.
Ее величество дробь: это что такое
Дробями в математике называются числа, каждое из которых состоит из одной или более частей единицы. Такие дроби еще называют обыкновенными, либо простыми. Как правило, они записываются в виде двух чисел, которые разделены горизонтальной или слеш-чертой, она называется «дробной». Например: ½, ¾.
Верхнее, или первое из этих чисел - это числитель (показывает, сколько взято долей от числа), а нижнее, или второе - знаменатель (демонстрирует, на столько частей разделена единица).
Дробная черта фактически выполняет функции знака деления. К примеру, 7:9=7/9
Традиционно обыкновенные дроби меньше единицы. В то время как десятичные могут быть больше ее.

Для чего нужны дроби? Да для всего, ведь в реальном мире далеко не все числа целые. К примеру, две школьницы в столовой купили в складчину одну вкусную шоколадку. Когда они уже собрались делить десерт, встретили подружку и решили угостить и и ее. Однако теперь необходимо правильно разделить шоколадку, если учесть, что она состоит из 12 квадратиков.
Поначалу девчонки хотели разделить все поровну, и тогда каждой бы досталось по четыре кусочка. Но, раздумав, они решили угостить подружку, не 1/3, а 1/4 шоколадки. А поскольку школьницы плохо изучали дроби, то они не учли, что при подобном раскладе в результате у них останется 9 кусочков, которые очень плохо делятся на двоих. Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше.
Виды дробей: обыкновенные и десятичные
Все математические дроби делятся на два больших разряда: обыкновенные и десятичные. Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму.
Десятичной называют позиционную запись дроби числа, которая фиксируется на письме через запятую, без черточки или слеша. Например: 0,75, 0,5.
Фактически десятичная дробь идентична обыкновенной, однако, в ее знаменателе всегда единица с последующими нулями - отсюда произошло и ее название.
Число, предшествующее запятой, - это целая часть, а все находящееся после - дробная. Любую простую дробь можно перевести в десятичную. Так, указанные в предыдущем примере десятичные дроби можно записать как обычные: ¾ и ½.

Стоит отметить, что и десятичные, и обыкновенные дроби могут быть как положительными, так и отрицательными. Если перед ними стоит знак "-", данная дробь отрицательная, если "+" - то положительная.
Подвиды обыкновенных дробей
Есть такие виды дробей простых.

Подвиды десятичной дроби
В отличие от простой, десятичная дробь делится всего на 2 вида.
- Конечная - получила такое название из-за того, что после запятой у нее ограниченное (конечное) число цифр: 19,25.
- Бесконечная дробь - это число с нескончаемым количеством цифр после запятой. К примеру, при делении 10 на 3 результатом будет бесконечная дробь 3,333…
Сложение дробей
Проводить различные арифметические манипуляции с дробями немного сложнее, чем с обычными числами. Однако, если усвоить основные правила, решить любой пример с ними не составит особого труда.
Например: 2/3+3/4. Наименьшим общим кратным для них будет 12, следовательно, необходимо, чтобы в каждом знаменателе стояло это число. Для этого числитель и знаменатель первой дроби умножаем на 4, получается 8/12, аналогично поступаем со вторым слагаемым, но только множим на 3 - 9/12. Теперь можно легко решить пример: 8/12+9/12= 17/12. Получившаяся дробь - это неправильная величина, поскольку числитель больше знаменателя. Ее можно и нужно пребразовать в правильную смешанную, разделив 17:12= 1 и 5/12.
В случае, если слагаются смешанные дроби, сначала действия совершаются с целыми числами, а потом с дробными.
Если в примере присутствует десятичная дробь и обычная, необходимо, чтобы обе стали простыми, потом привести их к одному знаменателю и сложить. К примеру 3,1+1/2. Число 3,1 можно записать как смешанную дробь 3 и 1/10 или как неправильную - 31/10. Общим знаменателем для слагаемых будет 10, поэтому нужно умножить поочередно числитель и знаменатель 1/2 на 5, получается 5/10. Далее можно легко все высчитать: 31/10+5/10=35/10. Полученный результат - неправильная сократимая дробь, приводим ее в нормальный вид, сократив на 5: 7/2=3 и 1/2, или десятичной - 3,5.
Если слагать 2 десятичные дроби, важно, чтобы после запятой было одинаковое количество цифр. Если это не так, нужно просто дописать необходимое количество нулей, ведь в десятичной дроби это можно сделать безболезненно. Например, 3,5+3,005. Чтобы решить это задание, нужно к первому числу прибавить 2 ноля и далее поочередно слагать: 3,500+3,005=3,505.
Вычитание дробей
Вычитая дроби, стоит поступать так же, как и при сложении: свести к общему знаменателю, отнять один числитель от другого, при необходимости перевести результат в смешанную дробь.

Например: 16/20-5/10. Общим знаменателем будет 20. Нужно привести вторую дробь к этому знаменателю, умножив обе ее части на 2, получается 10/20. Теперь можно решать пример: 16/20-10/20= 6/20. Однако этот результат относится к сократимым дробям, поэтому стоит поделить обе части на 2 и получается результат - 3/10.
Умножение дробей
Деление и умножение дробей - значительно более простые действия, нежели сложение и вычитание. Дело в том, что, выполняя эти задания, нет необходимости искать общий знаменатель.
Чтобы умножить дроби, нужно просто поочередно перемножить между собою оба числителя, а затем и оба знаменателя. Получившийся результат сократить, если дробь - это сократимая величина.

Например: 4/9х5/8. После поочередного умножения получается такой результат 4х5/9х8=20/72. Такая дробь сократима на 4, поэтому конечный ответ в примере - 5/18.
Как делить дроби
Деление дробей - тоже несложное действие, фактически оно все равно сводится к их умножению. Чтобы разделить одну дробь на другую, нужно вторую перевернуть и умножить на первую.

Например, деление дробей 5/19 и 5/7. Чтобы решить пример, нужно поменять местами знаменатель и числитель второй дроби и умножить: 5/19х7/5=35/95. Результат можно сократить на 5 - получается 7/19.
В случае, если необходимо разделить дробь на простое число, методика немного отличается. Изначально стоит записать это число как неправильную дробь, а потом делить по той же схеме. Например, 2/13:5 нужно записать как 2/13: 5/1. Теперь нужно перевернуть 5/1 и умножить получившиеся дроби: 2/13х1/5= 2/65.
Иногда приходится совершать деление дробей смешанных. С ними нужно поступать, как и с целыми числами: превратить в неправильные дроби, перевернуть делитель и умножить все. Например, 8 ½: 3. Превращаем все в неправильные дроби: 17/2: 3/1. Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную - 2 целых и 5/6.
Итак, разобравшись с тем, что такое дроби и как можно с ними совершать различные арифметические действия, нужно постараться не забывать об этом. Ведь люди всегда более склонны делить что-то на части, нежели прибавлять, поэтому нужно уметь делать это правильно.
Основное свойство дроби
Условимся считать, что под "действиями с дробями" на нашем уроке будут пониматься действия с обыкновенными дробями. Обыкновенная дробь - это дробь, обладающая такими атрибутами, как числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается из обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой, отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби особых затруднений не вызывают. Итак, вперёд!
Две дроби и называются равными, если .
Например, , так как
Равными также являются дроби и (так как ), и (так как).
Очевидно, равными являются и дроби и . Это означает, что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной: .
Это свойство называется основным свойством дроби.
Основное свойство дроби можно использовать для перемены знаков у числителя и знаменателя дроби. Если числитель и знаменатель дроби умножить на -1, то получим . Таким образом, значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
Сокращение дробей
Пользуясь основным свойством дроби, можно заменить данную дробь другой дробью, равной данной, но с меньшим числителем и знаменателем. Такую замену называют сокращением дроби.
Пусть, например, дана дробь . Числа 36 и 48 имеют наибольший общий делитель 12. Тогда
![]() .
.
В общем случае сокращение дроби возможно всегда, если числитель и знаменатель не являются взаимно простыми числами. Если числитель и знаменатель - взаимно простые числа, то дробь называется несократимой.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел .
Итак, сократить дробь - это значит разделить числитель и знаменатель дроби на общий множитель. Всё вышесказанное применимо и к дробным выражениям, содержащим переменные.
Пример 1. Сократить дробь
Решение. Для разложения числителя на множители, представив предварительно одночлен - 5xy в виде суммы - 2xy - 3xy , получим

Для разложения знаменателя на множители используем формулу разности квадратов:
Таким образом,
![]() .
.

Приведение дробей к общему знаменателю
Пусть даны две дроби и . Они имеют разные знаменатели: 5 и 7. Пользуясь основным свойством дроби, можно заменить эти дроби другими, равными им, причём такими, что у полученных дробей будут одинаковые знаменатели. Умножив числитель и знаменатель дроби на 7, получим
Умножив числитель и знаменатель дроби на 5, получим
Итак, дроби приведены к общему знаменателю:
![]() .
.
Но это не единственное решение поставленной задачи: например, данные дроби можно привести также к общему знаменателю 70:
![]() ,
,
![]()
и вообще к любому знаменателю, делящемуся одновременно на 5 и 7.
Рассмотрим ещё один пример: приведём к общему знаменателю дроби и . Рассуждая, как в предыдущем примере, получим
![]() ,
,
![]() .
.
Но в данном случае можно привести дроби к общему знаменателю, меньшему, чем произведение знаменателей этих дробей. Найдём наименьшее общее кратное чисел 24 и 30: НОК(24, 30) = 120.
Так как 120:4=5, то чтобы записать дробь со знаменателем 120, надо и числитель, и знаменатель умножить на 5, это число называется дополнительным множителем. Значит ![]() .
.
Далее, получаем 120:30=4. Умножив числитель и знаменатель дроби на дополнительный множитель 4, получим ![]() .
.
Итак, данные дроби приведены к общему знаменателю.
Для дробных выражений, в которые входят переменные, общим знаменателем является многочлен, который делится на знаменатель каждой дроби.
Пример 2. Найти общий знаменатель дробей и .
Решение. Общим знаменателем данных дробей является многочлен , так как он делится и на , и на . Однако этот многочлен не единственный, который может быть общим знаменателем данных дробей. Им может быть также многочлен ![]() , и многочлен
, и многочлен ![]() , и многочлен
, и многочлен ![]() и т.д. Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без остатка. Такой знаменатель называется наименьшим общим знаменателем.
и т.д. Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без остатка. Такой знаменатель называется наименьшим общим знаменателем.
В нашем примере наименьший общий знаменатель равен . Получили:
Нам удалось привести дроби к наименьшему общему знаменателю. Это произошло путём умножения числителя и знаменателя первой дроби на , а числителя и знаменателя второй дроби - на . Многочлены и называются дополнительными множителями, соответственно для первой и для второй дроби.
Сложение и вычитание дробей
Сложение дробей определяется следующим образом:
Например,
Если b = d , то
Это значит, что для сложения дробей с одинаковым знаменателем достаточно сложить числители, а знаменатель оставить прежним. Например,
Теперь рассмотрим пример сложения дробных выражений с переменными.
Пример 3. Преобразовать в одну дробь выражение
Решение. Найдём наименьший общий знаменатель. Для этого сначала разложим знаменатели на множители:
Наименьший общий знаменатель:
Дополнительные множители, на которые умножаются числители дробей:
Умножение и деление дробей
Произведение двух дробей и равно дроби, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей, т. е. .
Например,
При делении дроби на дробь числитель делимого умножается на знаменатель делителя, а знаменатель делимого - на числитель делителя, т. е. .
Например,
Свойства пропорции
1. Произведение крайних членов пропорции равно произведению её средних членов, т. е. если , то .
2. Из пропорции вытекают следующие пропорции: , , , т. е. в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
3. Чтобы найти неизвестный средний (крайний) член пропорции, нужно произведение крайних (средних) членов пропорции разделить на известный средний (крайний) член пропорции: и
Часть единицы или несколько ее частей называют простой или обыкновенной дробью. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей - числителем. Дробь записывается в виде:
В данном случае а - числитель, b - знаменатель.
Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью. Если числитель больше знаменателя, то дробь больше 1, тогда дробь называется неправильной.
Если числитель и знаменатель дроби равны, то дробь равна.
1. Если числитель можно разделить на знаменатель, то эта дробь равна частному от деления:
В случае если деление выполняется с остатком, то эта неправильная дробь может быть представлена смешанным числом, например:
Тогда 9 - неполное частное (целая часть смешанного числа),
1 - остаток (числитель дробной части),
5 - знаменатель.
Для того чтобы обратить смешанное число в дробь, необходимо умножить целую часть смешанного числа на знаменатель и прибавить числитель дробной части.
Полученный результат будет числителем обыкновенной дроби, а знаменатель останется прежним.
Действия с дробями
Расширение дроби.
Значение дроби не меняется, если умножить ее числитель и знаменатель на одно и то же число, отличное от нуля.
Например
:![]()
Сокращение дроби.
Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля.
Например
: ![]()
Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:
Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, то есть привести к общему знаменателю. Рассмотрим, например, следующие дроби: 
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того чтобы сложить дроби, необходимо сложить их числители, а для того чтобы вычесть дроби, надо вычесть их числители. Полученная сумма или разность будет числителем результата, а знаменатель останется прежним. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел сначала необходимо преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется к виду смешанного числа.
Умножение дробей . Для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.
Деление дробей . Для того чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь.
Десятичная дробь - это результат деления единицы на десять, сто, тысячу и т.д. частей. Сначала пишется целая часть числа, затем справа ставится десятичная точка. Первая цифра после десятичной точки означает число десятых, вторая - число сотых, третья - число тысячных и т. д. Цифры, расположенные после десятичной точки, называются десятичными знаками.
Например:
![]()
Свойства десятичных дробей
Свойства:
- Десятичная дробь не меняется, если справа добавить нули: 4,5 = 4,5000.
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: 0,0560000 = 0,056.
- Десятичная дробь возрастает в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиции вправо: 4,5 45 (дробь возросла в 10 раз).
- Десятичная дробь уменьшается в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиции влево: 4,5 0,45 (дробь уменьшилась в 10 раз).
Периодическая десятичная дробь содержит бесконечно повторяющуюся группу цифр, называемую периодом: 0,321321321321…=0,(321)
Действия с десятичными дробями
Сложение и вычитание десятичных дробей выполняются так же, как и сложение и вычитание целых чисел, необходимо только записать соответствующие десятичные знаки один под другим.
Например:
Умножение десятичных дробей проводится в несколько этапов:
- Перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку.
- Применяется правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях.
Например :
Сумма чисел десятичных знаков в сомножителях равна: 2+1=3. Теперь необходимо с конца получившегося числа отсчитать 3 знака и поставить десятичную точку: 0,675.
Деление десятичных дробей. Деление десятичной дроби на целое число: если делимое меньше делителя, тогда нужно записать ноль в целой части частного и поставить после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединить к его целой части следующую цифру дробной части и опять сравнить полученную целую часть делимого с делителем. Если новое число опять меньше делителя, надо повторить операцию. Этот процесс повторяется до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему, сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел.
Деление одной десятичной дроби на другую: сначала переносятся десятичные точки в делимом и делителе на число десятичных знаков в делителе, то есть делаем делитель целым числом, и выполняются действия, описанные выше.
Для того чтобы обратить десятичную дробь в обыкновенную, необходимо в качестве числителя взять число, стоящее после десятичной точки, а в качестве знаменателя взять k-ую степень десяти (k - количество десятичных знаков). Отличная от нуля целая часть сохраняется в обыкновенной дроби; нулевая целая часть опускается.
Например:
![]()
Для того чтобы обратить обыкновенную дробь в десятичную, надо разделить числитель на знаменатель в соответствии с правилами деления.
Процент - это сотая часть единицы, например: 5% означает 0,05. Отношение - это частное от деления одного числа на другое. Пропорция - это равенство двух отношений.
Например:
Основное свойство пропорции: произведение крайних членов пропорции равно произведению ее средних членов, то есть 5х30=6х25. Две взаимно зависимых величины называются пропорциональными, если отношение их величин сохраняется неизменным (коэффициент пропорциональности).
Таким образом, выявлены следующие арифметические действия.
Например:

Множество рациональных чисел включает в себя положительные и отрицательные числа (целые и дробные) и ноль. Более точное определение рациональных чисел, принятое в математике, следующее: число называется рациональным, если оно может быть представлено в виде обыкновенной несократимой дроби вида:, где a и b целые числа.
Для отрицательного числа абсолютная величина (модуль) - это положительное число, получаемое от перемены его знака с «-» на «+»; для положительного числа и нуля - само это число. Для обозначения модуля числа используются две прямые черты, внутри которых записывается это число, например: |–5|=5.
Свойства абсолютной величины
Пусть дан модуль числа  , для которого справедливы свойства:
, для которого справедливы свойства:
Одночлен - это произведение двух или нескольких сомножителей, каждый из которых либо число, либо буква, либо степень буквы: 3 х a х b. Коэффициентом чаще всего называют лишь числовой множитель. Одночлены называются подобными, если они одинаковы или отличаются лишь коэффициентами. Степень одночлена - это сумма показателей степеней всех его букв. Если среди суммы одночленов есть подобные, то сумма может быть приведена к более простому виду: 3 х a х b + 6 х a = 3 х a х (b + 2). Эта операция называется приведением подобных членов или вынесением за скобки.
Многочлен - это алгебраическая сумма одночленов. Степень многочлена есть наибольшая из степеней одночленов, входящих в данный многочлен.
Существуют следующие формулы сокращенного умножения:

Методы разложения на множители:

Алгебраическая дробь - это выражение вида , где A и B могут быть числом, одночленом, многочленом.
Если два выражения (числовые и буквенные) соединены знаком «=», то говорят, что они образуют равенство. Любое верное равенство, справедливое при всех допустимых числовых значениях входящих в него букв, называется тождеством.
Уравнение - это буквенное равенство, которое справедливо при определенных значениях входящих в него букв. Эти буквы называются неизвестными (переменными), а их значения, при которых данное уравнение обращается в тождество, - корнями уравнения.
Решить уравнение - значит найти все его корни. Два или несколько уравнений называются равносильными, если они имеют одни и те же корни.

- ноль являлся корнем уравнения;
- уравнение имело только конечное число корней.
Основные типы алгебраических уравнений:
У линейного уравнения ax + b = 0:
- если a х 0, имеется единственный корень x = -b/a;
- если a = 0, b ≠ 0, нет корней;
- если a = 0, b = 0, корнем является любое действительное число.
Уравнение xn = a, n N:
- если n - нечетное число, имеет при любом а действительный корень, равный a/n;
- если n - четное число, то при a 0, то имеет два корня.
Основные тождественные преобразования: замена одного выражения другим, тождественно равным ему; перенос членов уравнения из одной стороны в другую с обратными знаками; умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля.
Линейным уравнением с одним неизвестным называется уравнение вида: ax+b=0, где a и b - известные числа, а x - неизвестная величина.
Системы двух линейных уравнений с двумя неизвестными имеют вид:
Где a, b, c, d, e, f - заданные числа; x, y - неизвестные.
Числа a, b, c, d - коэффициенты при неизвестных; e, f - свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами: метод подстановки: из одного уравнения выражаем одно из неизвестных через коэффициенты и другое неизвестное, а затем подставляем во второе уравнение, решая последнее уравнение, находим сначала одно неизвестное, затем подставляем найденное значение в первое уравнение и находим второе неизвестное; метод сложения или вычитания одного уравнения из другого.
Операции с корнями:

Арифметическим корнем n-й степени из неотрицательного чис-ла a называется неотрицательное число, n-я степень которого рав-на a. Алгебраическим корнем n-й степени из данного числа называ-ется множество всех корней из этого числа.
Иррациональные числа в отличие от рациональных не могут быть представлены в виде обыкновенной несократимой дроби вида m/n, где m и n - целые числа. Это числа нового типа, которые могут быть вычислены с любой точностью, но не могут быть заменены рациональным числом. Они могут появиться как результат геометрических измерений, например: отношение длины диагонали квадрата к длине его стороны равно.
Квадратное уравнение есть алгебраическое уравнение второй степени ax2+bx+c=0, где a, b, c - заданные числовые или буквенные коэффициенты, x - неизвестное. Если разделить все члены этого уравнения на а, в результате получим x2+px+q=0 - приведенное уравнение p=b/a, q=c/a. Его корни находятся по формуле:
Если b2-4ac>0, тогда имеются два различных корня, b2- 4ac=0, тогда имеются два равных корня; b2-4ac Уравнения, содержащие модули
Основные типы уравнений, содержащие модули:
1) |f(x)| = |g(x)|;
2) |f(x)| = g(x);
3) f1(x)|g1(x)| + f2(x)|g2(x)| + … + fn(x)|gn(x)| =0, n N, где f(x), g(x), fk(x), gk(x) - заданные функции.


